خودرمزگذارها (Autoencoders)

در حین آموزش شبکه‌های عصبی پیچشی، یکی از چالش‌ها نیاز به حجم زیادی از داده‌های برچسب‌گذاری شده است. در زمینه طبقه‌بندی تصاویر، لازم است تصاویر را به کلاس‌های مختلف تقسیم‌بندی کنیم که این کار مستلزم صرف تلاش‌های دستی قابل توجهی است.

با این حال، ممکن است تمایل داشته باشیم از داده‌های خام (بدون برچسب) برای آموزش استخراج‌کننده‌های ویژگی CNN بهره‌برداری کنیم که به این روش یادگیری خودنظارتی گفته می‌شود. به‌جای استفاده از برچسب‌ها، ما از تصاویری که به‌عنوان ورودی و خروجی شبکه مورد استفاده قرار می‌گیرند، سود می‌بریم. ایده اصلی خودرمزگذار این است که یک شبکه انکودر داریم که تصویر ورودی را به یک فضای نهان تبدیل می‌کند (که به‌طور معمول پیوستاری با اندازه کوچکتر است) و سپس یک شبکه دیکودر وجود دارد که هدف آن بازسازی تصویر اصلی است.

✅ خودرمزگذار یک نوع شبکه عصبی مصنوعی است که به منظور یادگیری کدگذاری‌های کارآمد از داده‌های بدون برچسب به کار می‌رود.

از آنجایی که ما یک خودرمزگذار را آموزش می‌دهیم تا تا حد ممکن اطلاعات را از تصویر اصلی حفظ کرده و بازسازی دقیقتری انجام دهد، شبکه تلاش می‌کند تا بهترین نمایش از تصاویر ورودی را برای ضبط معانی پیدا کند.

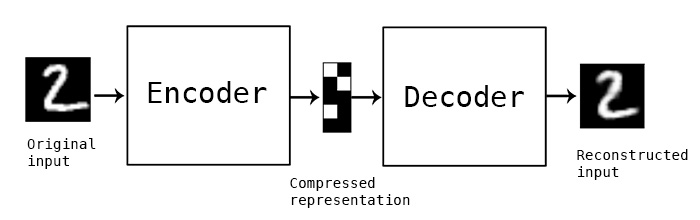
نمودار خودرمزگذار

تصویر از وبلاگ Keras

سناریوهایی برای استفاده از اتو انکودرها

اگرچه بازسازی تصاویر اصلی به‌تنهایی به‌نظر مفید می‌رسد، اما چندین سناریو وجود دارد که در آن‌ها اتو انکودرها به‌خصوص کارآمد هستند:

کاهش بعد تصاویر به منظور تجسم یا آموزش نمایش‌های تصویری. معمولاً اتو انکودرها نتایج بهتری نسبت به تحلیل مؤلفه‌های اصلی (PCA) به‌دست می‌دهند، چرا که به طبیعت فضایی تصاویر و ویژگی‌های سلسله‌مراتبی آن‌ها توجه دارند.
کاهش نویز، به‌عبارتی حذف نویز از تصاویر. به دلیل این‌که نویز اطلاعات زیادی را به‌طور بیهوده حمل می‌کند، اتو انکودر قادر به ذخیره‌سازی تمام این اطلاعات در فضای نهان نسبتاً کوچک نیست و بنابراین تنها بخش‌های مهم تصویر را حفظ می‌کند. در فرآیند آموزش کاهش‌دهنده‌های نویز، ما با تصاویر اصلی آغاز می‌کنیم و از تصاویر با نویز مصنوعی به‌عنوان ورودی برای اتو انکودر استفاده می‌نماییم.
افزایش وضوح، به‌معنای افزایش کیفیت تصاویر. ما با تصاویر با وضوح بالا آغاز کرده و از تصاویر با وضوح پایین به‌عنوان ورودی اتو انکودر بهره می‌گیریم.
مدل‌های تولیدی. پس از آموزش اتو انکودر، می‌توانیم از بخش دیکودر برای تولید اشیاء جدید با شروع از بردارهای نهان تصادفی استفاده کنیم.

خودرمزگذارهای متغیر (VAE)

خودرمزگذارهای سنتی به نوعی ابعاد داده‌های ورودی را کاهش می‌دهند و ویژگی‌های اساسی تصاویر ورودی را شناسایی می‌کنند. با این حال، وکتورهای نهفته معمولاً معنای مشخصی ندارند. به عبارت دیگر، با استفاده از مجموعه داده MNIST به عنوان مثال، شناسایی این که کدام ارقام با وکتورهای نهفته مختلف مربوط هستند، کار آسانی نیست، زیرا وکتورهای نهفته نزدیک لزوماً به همان ارقام تعلق ندارند.

از سوی دیگر، برای آموزش مدل‌های تولیدی بهتر است که درکی از فضای نهفته داشته باشیم. این ایده ما را به خودرمزگذارهای متغیر (VAE) می‌رساند.

VAE یک خودرمزگذار است که یاد می‌گیرد تا توزیع آماری پارامترهای نهفته را پیش‌بینی کند، که به آن توزیع نهفته اطلاق می‌شود. به عنوان مثال، ممکن است بخواهیم وکتورهای نهفته به صورت نرمال با مقداری میانگین z_mean و انحراف استاندارد z_sigma (که هر دو میانگین و انحراف استاندارد، وکتورهایی از ابعاد خاصی هستند) توزیع شوند. انکودر در VAE می‌آموزد که این پارامترها را پیش‌بینی کند و سپس دکودر از این توزیع یک وکتور تصادفی را انتخاب کرده و شیء را بازسازی نماید.

خودرمزگذار متغیر (VAE) مدلی است که به یادگیری توزیع آماری پارامترهای نهان، تحت عنوان توزیع نهان، می‌پردازد. به‌عنوان مثال، ممکن است بخواهیم وکتورهای نهان به‌طور نرمال با میانگین z_mean و انحراف معیار z_sigma (که هر دو میانگین و انحراف معیار وکتورهایی با ابعاد d هستند) توزیع شوند. در این مدل، انکودر یاد می‌گیرد که این پارامترها را پیش‌بینی نماید و سپس دیکودر از یک وکتور تصادفی حاصل از این توزیع برای بازسازی شیء مورد نظر استفاده می‌کند.

به‌اختصار:

از وکتور ورودی، z_mean و z_log_sigma پیش‌بینی می‌شود (به‌جای پیش‌بینی انحراف معیار خود، لگاریتم آن پیش‌بینی خواهد شد).
از توزیع N(z_mean, exp(z_{log_sigma})) یک وکتور sample نمونه‌برداری می‌شود.
دیکودر تلاش می‌کند تصویر اصلی را با استفاده از sample به‌عنوان ورودی بازسازی نماید.

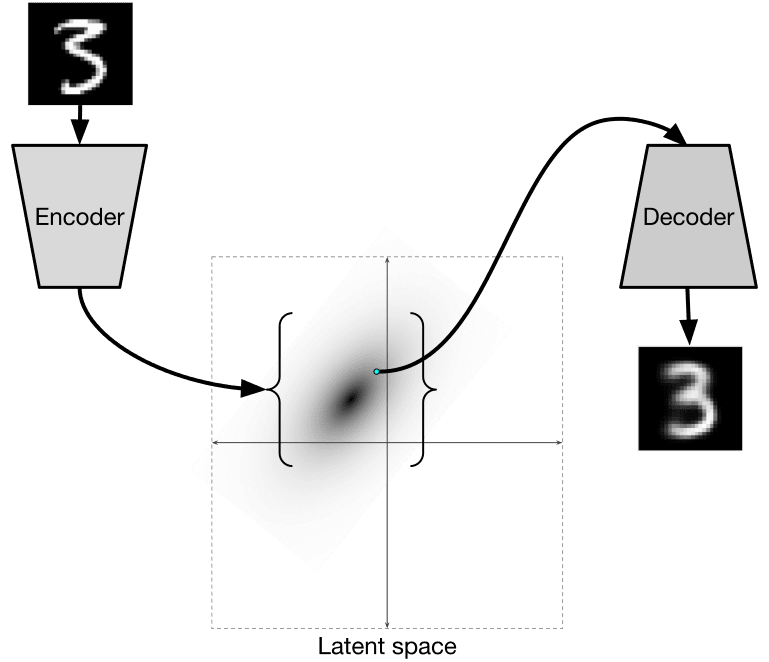
تصویر از این وبلاگ به‌دست ایزاک دیکمن

خودرمزگذارهای متغیر از تابع هزینه‌ای پیچیده‌ای استفاده می‌کنند که از دو بخش تشکیل شده است:

هزینه بازسازی که تابع هزینه‌ای است که نشان می‌دهد یک تصویر بازسازی‌شده چقدر به هدف نزدیک است (این معمولاً می‌تواند خطای میانگین مربعات، یا MSE، باشد). این تابع هزینه مشابه تابع هزینه در اتوانکودرهای معمولی است.
هزینه KL که اطمینان می‌دهد که توزیع‌های متغیرهای نهان به توزیع نرمال نزدیک بمانند. این بر اساس مفهوم انحراف کولیبا-لیبر - معیاری برای برآورد شباهت دو توزیع آماری - بنا شده است.

یکی از مزایای مهم VAE این است که به ما اجازه می‌دهد تا به سادگی تصاویر جدیدی تولید کنیم، زیرا می‌دانیم که از کدام توزیع باید نمایه‌های نهفته را نمونه‌برداری کنیم. به عنوان مثال، اگر VAE را با نمایه نهفته دو بعدی بر روی MNIST آموزش دهیم، می‌توانیم سپس اجزای نمایه نهفته را تغییر دهیم تا ارقام مختلفی را به دست آوریم:

تصویر از دیمیتری سوشنیکوف

توجه فرمایید که چگونه تصاویر به یکدیگر متصل می‌شوند، زیرا ما شروع به برداشت نمایه‌های نهفته از بخش‌های مختلف فضای پارامتر نهفته می‌کنیم. همچنین می‌توانیم این فضا را در دو بعد تجسم نماییم:

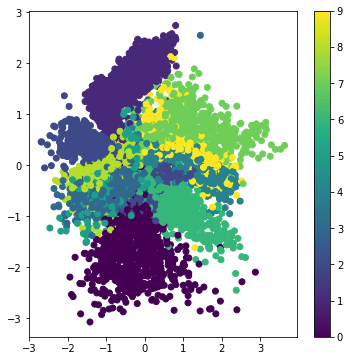
تصویر از دیمیتری سوشنیکوف

✍️ تمرینات: خودرمزگذارها

برای آشنایی بیشتر با خودرمزگذارها، به این نوت‌بوک‌های مرتبط مراجعه نمایید:

ویژگی‌های خودرمزگذارها

ویژه داده - آن‌ها به خوبی تنها با نوع تصاویری که بر روی آن‌ها آموزش دیده‌اند، کار می‌کنند. به عنوان مثال، اگر یک شبکه سوپر رزولوشن را بر روی گل‌ها آموزش دهیم، به خوبی بر روی پرتره‌ها عمل نخواهد کرد. این به این خاطر است که شبکه می‌تواند تصویر با وضوح بالا را با برداشت جزئیات ریز از ویژگی‌های آموخته‌شده از مجموعه داده آموزشی تولید نماید.
از دست رفتگی - تصویر بازسازی‌شده به اندازه تصویر اصلی نیست. ماهیت از دست رفتگی توسط تابع از دست رفتگی تعریف می‌شود که در زمان آموزش استفاده می‌گردد.
بر روی داده‌های بدون برچسب کار می‌کند.

نتیجه‌گیری

در این درس، شما با انواع مختلف خودرمزگذارها که برای دانشمندان هوش مصنوعی در دسترس هستند، آشنا شدید. شما یاد گرفتید که چگونه این سیستم‌ها را ایجاد کنید و از آنها برای بازسازی تصاویر بهره ببرید. همچنین با مدل های VAE آشنا شده و نحوه استفاده از آن برای تولید تصاویر جدید را فراگرفتید.

چالش

در این درس، شما درباره‌ی استفاده از خودرمزگذارها در زمینه‌ی تصاویر یاد گرفتید. اما این سیستم‌ها می‌توانند در حوزه‌ی موسیقی نیز مورد استفاده قرار گیرند! به پروژه‌ی MusicVAE از پروژه‌ی Magenta نگاهی بیندازید، که از خودرمزگذارها جهت یادگیری بازسازی موسیقی بهره می‌برد. با این کتابخانه چند آزمایش انجام دهید تا ببینید چه نتایجی می‌توانید خلق کنید.

مرور و مطالعه خودآموز

برای مرجع بیشتر، می‌توانید با خودرمزگذارها در منابع زیر آشنا شوید:

تکلیف

در انتهای این نوت‌بوک با استفاده از TensorFlow، شما یک 'وظیفه' خواهید یافت - از این به‌عنوان تکلیف خود استفاده نمایید.