مقدمهای بر شبکههای عصبی: پرسپترون چند لایه
در بخش پیشین، شما با ابتداییترین مدل شبکه عصبی - پرسپترون تک لایه، که یک مدل خطی دستهبندی دو کلاسه است - آشنا شدید.
در این بخش، ما این مدل را به یک چارچوب منعطفتر ارتقا خواهیم داد که به ما امکان میدهد:
- علاوه بر دستهبندی دو کلاسه، دستهبندی چند کلاسه را نیز به انجام برسانیم.
- علاوه بر دستهبندی، مسائل رگرسیون را نیز حل نماییم.
- کلاسهایی که به صورت خطی قابل تفکیک نیستند را از یکدیگر جدا کنیم.
ما همچنین چارچوب مدولار خود را در زبان برنامهنویسی پایتون توسعه خواهیم داد که به ما اجازه میدهد معماریهای متنوع شبکه عصبی را ایجاد کنیم.
فرمولبندی یادگیری ماشین
اجازه دهید با فرمولبندی مسئله یادگیری ماشین آغاز کنیم. فرض کنید یک مجموعه داده آموزشی X با برچسبهای Y در اختیار داریم و نیازمند ساخت یک مدل f هستیم که دقیقترین پیشبینیها را انجام دهد. کیفیت پیشبینیها با استفاده از تابع زیان ℒ اندازهگیری میشود. توابع زیان زیر به طور معمول مورد استفاده قرار میگیرند:
- برای مسئله رگرسیون، زمانی که نیاز به پیشبینی یک عدد داریم، میتوانیم از خطای مطلق
∑i|f(x(i))-y(i)|، یا خطای مربعی∑i(f(x(i))-y(i))2استفاده کنیم. - برای دستهبندی، از زیان 0-1 (که در اصل همان دقت مدل است)، یا زیان لجستیک استفاده میکنیم.
برای پرسپترون تک لایه، تابع f به عنوان یک تابع خطی f(x)=wx+b تعریف شده است (در اینجا w ماتریس وزن، x بردار ویژگیهای ورودی و b بردار بایاس است). برای معماریهای مختلف شبکه عصبی، این تابع میتواند شکل پیچیدهتری به خود بگیرد.
در مسئلهی طبقهبندی، غالباً مطلوب است که احتمال کلاسهای مربوطه را به عنوان خروجی شبکه به دست آوریم. برای تبدیل اعداد اختیاری به احتمالات (برای مثال، جهت نرمالسازی خروجی)، معمولاً از تابع softmax با نماد σ استفاده میکنیم و تابع f به صورت f(x)=σ(wx+b) تعریف میشود.
در تعریف تابع f در بالا، w و b به عنوان پارامترها با نماد θ=⟨w,b⟩ شناخته میشوند. با در اختیار داشتن مجموعه داده ⟨X,Y⟩، میتوانیم یک خطای کلی را بر روی کل مجموعه داده به عنوان تابعی از پارامترها θ محاسبه نماییم.
✅ هدف از فرآیند آموزش شبکه عصبی، کمینهسازی خطا از طریق تغییر پارامترها θ میباشد
بهینهسازی گرادیان کاهشی
یک روش شناختهشده برای بهینهسازی تابع، گرادیان کاهشی نام دارد. ایده اصلی این است که میتوانیم مشتق (در حالت چندبعدی به نام گرادیان) تابع زیان را نسبت به پارامترها محاسبه کنیم و پارامترها را به گونهای تغییر دهیم که خطا کاهش یابد. این فرآیند را میتوان به صورت زیر فرمولبندی کرد:
- پارامترها را با مقادیر تصادفی اولیه w(0) و b(0) مقداردهی کنید.
- گام زیر را چندین بار تکرار نمایید:
w(i+1) = w(i) - η * (∂ℒ/∂w)b(i+1) = b(i) - η * (∂ℒ/∂b)
در طول فرآیند آموزش، گامهای بهینهسازی باید با در نظر گرفتن کل مجموعه داده محاسبه شوند (به یاد داشته باشید که زیان به عنوان مجموع در تمام نمونههای آموزشی محاسبه میشود). با این حال، در عمل، ما بخشهای کوچکی از مجموعه داده به نام مینیبچها را در نظر میگیریم و گرادیانها را بر اساس زیرمجموعهای از دادهها محاسبه میکنیم. از آنجا که زیرمجموعه هر بار به صورت تصادفی انتخاب میشود، چنین روشی گرادیان کاهشی تصادفی (SGD) نامیده میشود.
شبکههای پرسپترون چند لایه و پسانتشار
شبکه تک لایه، همانگونه که پیشتر مشاهده کردیم، قادر به طبقهبندی کلاسهای جداشدنی خطی است. برای ایجاد یک مدل پیچیدهتر، میتوانیم چندین لایه از شبکه را با یکدیگر ترکیب کنیم. از نظر ریاضی، این به معنای آن است که تابع f شکل پیچیدهتری خواهد داشت و در چند مرحله محاسبه میشود:
z1 = w1x + b1z2 = w2α(z1) + b2f = σ(z2)
در اینجا، α یک تابع فعالسازی غیرخطی، σ یک تابع softmax و پارامترها θ=<w1,b1,w2,b2> هستند.
الگوریتم گرادیان کاهشی بدون تغییر باقی میماند، اما محاسبه گرادیانها پیچیدهتر خواهد بود. با توجه به قاعده مشتق زنجیرهای، میتوانیم مشتقها را به صورت زیر محاسبه کنیم:
∂ℒ/∂w2 = (∂ℒ/∂σ)(∂σ/∂z2)(∂z2/∂w2)∂ℒ/∂w1 = (∂ℒ/∂σ)(∂σ/∂z2)(∂z2/∂α)(∂α/∂z1)(∂z1/∂w1)
✅ قاعده مشتق زنجیرهای برای محاسبه مشتقهای تابع زیان نسبت به پارامترها به کار میرود.
توجه داشته باشید که قسمت چپترین همه این عبارات یکسان است، بنابراین میتوانیم مشتقها را به طور موثر با شروع از تابع زیان و حرکت "به عقب" در نمودار محاسباتی محاسبه کنیم. بنابراین روش آموزش یک پرسپترون چند لایه پسانتشار یا 'backprop' نامیده میشود.
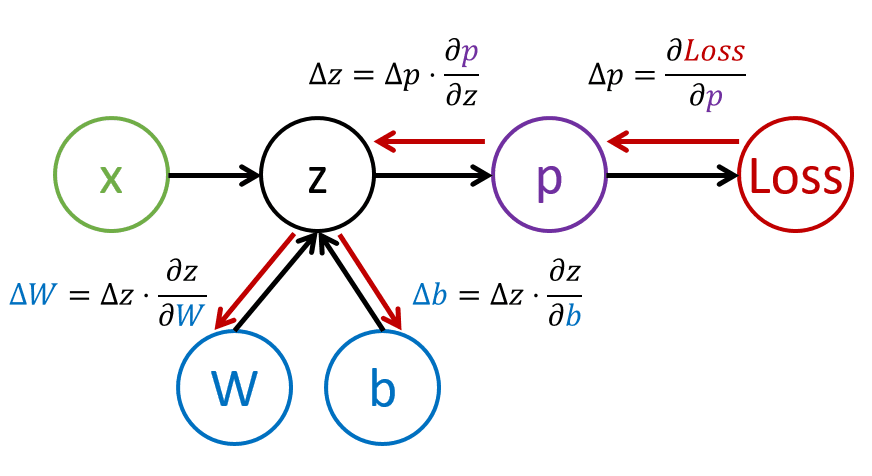
TODO: منبع تصویر ذکر شود
✅ در مثال دفترچه یادداشت، پسانتشار را با جزئیات بیشتری پوشش خواهیم داد.
نتیجهگیری
در این درس، ما کتابخانه شبکه عصبی خود را ایجاد کردیم و از آن برای یک کار طبقهبندی دوبعدی ساده استفاده نمودیم.
🚀 چالش
در نوتبوک همراه، شما چارچوب خود را برای ساخت و آموزش پرسپترونهای چند لایه پیادهسازی خواهید کرد. شما قادر خواهید بود جزئیات نحوه عملکرد شبکههای عصبی مدرن را مشاهده نمایید.
به دفترچه OwnFramework مراجعه کرده و آن را تکمیل نمایید.
مرور و مطالعه شخصی
پسانتشار یک الگوریتم رایج در هوش مصنوعی و یادگیری ماشین است که مطالعه آن با جزئیات بیشتر ارزشمند است.