→ بازگشت به شبکه‌های عصبی

مقدمه‌ای بر شبکه‌های عصبی:‌ پرسپترون

یکی از نخستین کوشش‌ها برای پیاده‌سازی چیزی مشابه با یک شبکه عصبی مدرن، توسط فرانک روزنبلات از آزمایشگاه هوانوردی کرنل در سال ۱۹۵۷ صورت گرفت. این یک پیاده‌سازی سخت‌افزاری با نام "Mark-1" بود که برای تشخیص اشکال هندسی اولیه مانند مثلث‌ها، مربع‌ها و دایره‌ها طراحی شده بود.

تصاویر از ویکی‌پدیا

یک تصویر ورودی به وسیله‌ی آرایه‌ای از ۲۰x۲۰ فتوسل نمایش داده می‌شد، از این رو شبکه عصبی دارای ۴۰۰ ورودی و یک خروجی دودویی بود. یک شبکه ساده شامل یک نورون بود که به آن واحد منطق آستانه نیز گفته می‌شد. وزن‌های شبکه عصبی مانند پتانسیومترهایی عمل می‌کردند که در طول مرحله آموزش نیاز به تنظیم دستی داشتند.

✅ یک پتانسیومتر ابزاری است که به کاربر امکان تنظیم مقاومت در یک مدار را می‌دهد.

نیویورک تایمز در آن زمان در رابطه با پرسپترون چنین نوشت: نمونه‌ی اولیه یک رایانه‌ی الکترونیکی که [نیروی دریایی] انتظار دارد قادر به راه رفتن، صحبت کردن، دیدن، نوشتن، تکثیر خود و آگاهی از وجود خویش باشد.

مدل پرسپترون

فرض کنیم در مدل ما N ویژگی وجود دارد، در این صورت بردار ورودی یک بردار با اندازه N خواهد بود. یک پرسپترون یک مدل طبقه بندی دودویی است، یعنی می تواند بین دو کلاس از داده های ورودی تمایز قائل شود. ما فرض خواهیم کرد که برای هر بردار ورودی x، خروجی پرسپترون ما +1 یا -1 خواهد بود، بسته به کلاس. خروجی با استفاده از فرمول زیر محاسبه می شود:

y(x) = f(wTx)

که در آن f یک تابع فعال سازی گام به گام است

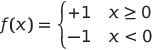
آموزش پرسپترون

برای آموزش یک پرسپترون، لازم است یک بردار وزن w بیابیم که بیشترین مقادیر را به درستی طبقه‌بندی کند، به عبارت دیگر، منجر به کمترین خطا شود. این خطا E توسط معیار پرسپترون به صورت زیر تعریف می‌گردد:

E(w) = -∑wTxiti

که در آن:

• مجموع بر روی آن نقاط داده آموزشی i گرفته می‌شود که منجر به طبقه‌بندی اشتباه می‌شوند
• xi داده ورودی است و ti برای نمونه‌های منفی و مثبت به ترتیب -1 یا +1 می‌باشد.

این معیار به عنوان یک تابع از وزن‌ها w در نظر گرفته می‌شود و ما نیاز به کمینه‌سازی آن داریم. اغلب، یک روش به نام gradient descent استفاده می‌شود، که در آن با برخی وزن‌های اولیه w⁽⁰⁾ شروع می‌کنیم و سپس در هر گام وزن‌ها را مطابق فرمول زیر به‌روزرسانی می‌کنیم:

w(t+1) = w(t) - η∇E(w)

در این رابطه، η به عنوان نرخ یادگیری شناخته می‌شود و ∇E(w) بیانگر گرادیان تابع E است. پس از محاسبه گرادیان، به فرمول زیر دست می‌یابیم:

w(t+1) = w(t) + ∑ηxiti

الگوریتم در زبان برنامه‌نویسی پایتون به صورت زیر است:

def train(positive_examples, negative_examples, num_iterations = 100, eta = 1):

    weights = [0,0,0] # Initialize weights (almost randomly :)
        
    for i in range(num_iterations):
        pos = random.choice(positive_examples)
        neg = random.choice(negative_examples)

        z = np.dot(pos, weights) # compute perceptron output
        if z < 0: # positive example classified as negative
            weights = weights + eta*weights.shape

        z  = np.dot(neg, weights)
        if z >= 0: # negative example classified as positive
            weights = weights - eta*weights.shape

    return weights

نتیجه‌گیری

در این درس، شما با مدل طبقه‌بندی دودویی به نام پرسپترون آشنا شدید و آموختید که چگونه با استفاده از یک بردار وزن، آن را آموزش دهید.

مرور و خودآموزی

برای مشاهده نحوه استفاده از پرسپترون در حل یک مسئله ساده و همچنین مسائل واقعی و برای ادامه یادگیری، به دفترچه پرسپترون مراجعه کنید.

همچنین، یک مقاله جالب درباره پرسپترون‌ها نیز وجود دارد.